kemarau
Anton atas membuat 100 buah teralis berbentuk juring lingkaran terbuat dari besi. Panjang jari-jari lingkaran 18 cm dengan besar sudut pusat $60^\circ$. Panjang besi minimal yg digunakan untuk membuat teralis tersebut adalah .... $(\pi=3,14)$
A. $169,56$ m
B. $54,84$ m
C. $36,00$ m
D. $18,84$ m
Pembahasan:
Bentuk teralis:
Panjang garis singgung persekutuan luar dua lingkaran yg berpusat di $P$ dengan $Q$ adalah 24 cm. Jika panjang jari-jari lingkaran kecil 4 cm dengan jarak titik pusat kedua lingkaran adalah 25 cm, maka panjang jari-jari lingkaran lainnya adalah ....
A. 7 cm
B. 10 cm
C. 11. cm
D. 12 cm
Pembahasan:
Perhatikan gambar berikut:
Panjang garis singgung persekutuan dalam dua lingkaran adalah 15 cm. Jika panjang jari-jari salah satu lingkaran adalah 6 cm dengan jarak kedua titik pusat lingkaran adalah 17 cm, maka panjang jari-jari lingkaran lainnya adalah ....
A. 2 cm
B. 3 cm
C. 4 cm
D. 8 cm
Pembahasan:
Perhatikan gambar ilustrasi berikut:
Diketahui:
➥ $R=6$ cm
➥ $|AB|=15$ cm
➥ $|PQ|=17$ cm
Dari gambar di atas, dengan menggunakan teorema pythagoras kita peroleh:
$\begin{align*}(R+r)^2&=|PQ|^2-|AB|^2\\(6+r)^2&=17^2-15^2\\(^+r)^2&=(17-15)(17+15)\\(6+r)^2&=64\\6+r&=\sqrt{64}\\6+r&=8\\r&=8-6\\r&=2\end{align*}$
Jadi, panjang jari-jari lingkaran lainnya adalah 2 cm.
Pada suatu lingkaran, besar sudut pusat $AOB=108^\circ$. Jika panjang jari-jari lingkaran tersebut 7 cm, maka panjang busur $AB$ adalah ....
A. 132 cm
B. 52,8 cm
C. 26,4 cm
D. 13,2 cm
Pembahasan:
$\begin{align*}\text{Panjang Busur}&=\frac{\text{sudut pusat}}{360^\circ}\times2\pi r\\&=\frac{108^\circ}{260^\circ}\times 2\times\frac{22}{7}\times 7\\&=\frac{3}{10}\times 2\times 22\\&=13,2\end{align*}$
Perhatikan gambar!
$P$ adalah titik pusat lingkaran. Luas juring $PLM=24$ $cm^2$, luas juring $PKN$ adalah ....
Pembahasan:
$\begin{align*}\frac{\text{luas }PKN}{\text{luas }PLM}&=\frac{\text{sudut pusat }PKN}{\text{sudut pusat }PLM}\\ \text{luas }PKN&=\frac{\text{sudut pusat }PKN}{\text{sudut pusat }PLM}\times \text{luas }PLM\\&=\frac{60^\circ}{45^\circ}\times 24\\&=\frac{4}{3}\times 24\\&=32\end{align*}$
Jadi, luas juring $PKN$ adalah 32 $cm^2$
Berikut ini soal dengan pembahasan Ujian Nasional (UN) Matematika SMP/MTS Materi Lingkaran, meliputi unsur-unsur lingkaran, Luas dengan Keliling lingkaran, Busur, juring, tembereng, sudut-sudut dengan lingkaran beserta hubungannya (sudut pusat dengan sudut keliling) dengan garis singgung persekutuan dalam dengan garis singgung persekutuan luar. Soal-soal saol yg disajikan di urut dari soal UN terbaru sampai soal UN beberapa tahun terakhir. Semoga Soal dengan Pembahasan Ujian Nasional Materi lingkaran ini, bisa membantu adik-adik mempersiapkan diri menghadapi Ujian Nasional 2020 yg atas datang
Soal No 1 [UN SMP/MTs 2020]
Keliling lingkaran adalah 44 cm, Luas lingkaran tersebut adalah ... $cm^2$
A. 77
B. 154
C. 616
D. 1.232
Pembahasan:
Diketahui:
Keliling lingkaran $(K)=44$
$\begin{align*}K&=44\\2\pi r&=44\\r&=\frac{44}{2\pi}\\r&=\frac{22}{\pi}\end{align*}$
Luas Lingkaran $(L)$
$\begin{align*}L&=\pi r^2\\&=\pi \left(\frac{22}{\pi}\right)^2\\&=\pi\times\frac{22^2}{\pi^2}\\&=\frac{22^2}{\pi}\\&=\frac{22^2}{\frac{22}{7}}\\&=22^2\times \frac{7}{22}\\&=22\times 7\\&=154\end{align*}$
Jawaban : B
Soal No 2 [UN SMP/MTs 2020]
Perhatikan gambar lingkaran berpusat di $O$ berikut!
Besar $\angle AOB=110^\circ$, besar $\angle BDC=$ ....
A. $80^\circ$
B. $70^\circ$
C. $55^\circ$
D. $35^\circ$
Pembahasan:
Perhatihan garis $AC$ berupa garis lurus, dengan demikian $\angle AOC=180^\circ$
$\begin{align*}\angle AOC&=\angle AOB +\angle BOC\\ \angle BOC&=\angle AOC-\angle AOB\\ \angle BOC&=180^\circ-110^\circ\\ \angle BOC&=70^\circ\end{align*}$
Perhatikan juga bahwa sudut keliling $\angle BDC $ dengan sudut pusat $\angle BOC$ menghadap busur yg sama, dengana demikian maka:
$\begin{align*}\angle BDC&=\frac{1}{2}\times \angle BOC\\&=\frac{1}{2}\times 70^\circ\\&=35^\circ\end{align*}$
Jawaban : D
Soal No 3 [UN SMP/MTs 2020]
Perhatikan gambar berikut!
Garis AB disebut ....
A. apotema
B. busur
C. juring
D. tali busur
Pembahasan :
Garis $AB$ disebut tali busur
Jawaban : D
Soal No 4 [UN SMP/MTs 2020]
Sebuah taman berbentuk juring lingkaran seperti tampak dengan gambar.
Di sekeliling taman atas dipasang pagar kawat 3 kali putaran. Panjang kawat minimal yg diperlukan adalah ....
A. 64 m
B. 132 m
C. 192 m
D. 258 m
Pembahasan:
$\begin{align*}\text{Panjang Busur}&=\frac{\text{sudut pusat}}{360^\circ}\times \text{Keliling Lingkaran}\\&=\frac{120^\circ}{360^\circ}\times 2\pi r\\&=\frac{1}{3}\times 2\times \frac{22}{7}\times 21\\&=44\end{align*}$
$\begin{align*}\text{Keliling bangun tersebut}&=\text{panjang busur}+2r\\&=44+2(21)\\&=44+42\\&=86\end{align*}$
Karena pagar kawat dipasang $3\times $ putaran, maka panjang kawat yg diperlukan adalah $3\times \text{Keliling}=3\times 86=258$ m
Karena pagar kawat dipasang $3\times $ putaran, maka panjang kawat yg diperlukan adalah $3\times \text{Keliling}=3\times 86=258$ m
jawaban : D
Soal No 5 [UN SMP/MTs 2020]
Anton atas membuat 100 buah teralis berbentuk juring lingkaran terbuat dari besi. Panjang jari-jari lingkaran 18 cm dengan besar sudut pusat $60^\circ$. Panjang besi minimal yg digunakan untuk membuat teralis tersebut adalah .... $(\pi=3,14)$
A. $169,56$ m
B. $54,84$ m
C. $36,00$ m
D. $18,84$ m
Pembahasan:
Bentuk teralis:
Misal keliling 1 buah teralis adalah $K$.
$\begin{align*}K&=\text{Panjang Busur}+2r\\&=\frac{60^\circ}{360^\circ}\times2\pi r+2r\\&=\frac{1}{6}\times 2\times 3,14\times 18+2(18)\\&=18,84+36\\&=54,84\end{align*}$
Panjang besi minimal yg diperlukan 1 teralis adalah $54,84$ cm, maka untuk 100 teralis teralis diperlukan $100\times 54,84=5484$ cm $=54,84$ m
Jawaban : B
Soal No 6 [UN SMP/MTs 2015]
Panjang garis singgung persekutuan luar dua lingkaran yg berpusat di $P$ dengan $Q$ adalah 24 cm. Jika panjang jari-jari lingkaran kecil 4 cm dengan jarak titik pusat kedua lingkaran adalah 25 cm, maka panjang jari-jari lingkaran lainnya adalah ....
A. 7 cm
B. 10 cm
C. 11. cm
D. 12 cm
Pembahasan:
Perhatikan gambar berikut:
Diketahui:
➥ $r=4$ cm
➥ $|PQ|=25$ cm
➥ $|AB|=24$ cm
Dari gambar di atas, dengan menggunakan teorema pythagoras, kita peroleh:
$\begin{align*}(R-r)^2&=|PQ|^2-|AB|^2\\(R-4)^2&=25^2-24^2\\(R-4)^2&=(25-24)(25+24)\\(R-4)^2&=49\\R-4&=\sqrt{49}\\R-4&=7\\R&=7+4\\R&=11\end{align*}$
Jadi, panjang jari-jari lingkaran lainnya adalah 11 cm
Jawaban : C
Soal No 7 [UN SMP/MTs 2015]
Panjang garis singgung persekutuan dalam dua lingkaran adalah 15 cm. Jika panjang jari-jari salah satu lingkaran adalah 6 cm dengan jarak kedua titik pusat lingkaran adalah 17 cm, maka panjang jari-jari lingkaran lainnya adalah ....
A. 2 cm
B. 3 cm
C. 4 cm
D. 8 cm
Pembahasan:
Perhatikan gambar ilustrasi berikut:
Diketahui:
➥ $R=6$ cm
➥ $|AB|=15$ cm
➥ $|PQ|=17$ cm
Dari gambar di atas, dengan menggunakan teorema pythagoras kita peroleh:
$\begin{align*}(R+r)^2&=|PQ|^2-|AB|^2\\(6+r)^2&=17^2-15^2\\(^+r)^2&=(17-15)(17+15)\\(6+r)^2&=64\\6+r&=\sqrt{64}\\6+r&=8\\r&=8-6\\r&=2\end{align*}$
Jadi, panjang jari-jari lingkaran lainnya adalah 2 cm.
Jawaban: A
Soal No 8 [UN SMP/MTs 2014]
Pada suatu lingkaran, besar sudut pusat $AOB=108^\circ$. Jika panjang jari-jari lingkaran tersebut 7 cm, maka panjang busur $AB$ adalah ....
A. 132 cm
B. 52,8 cm
C. 26,4 cm
D. 13,2 cm
Pembahasan:
$\begin{align*}\text{Panjang Busur}&=\frac{\text{sudut pusat}}{360^\circ}\times2\pi r\\&=\frac{108^\circ}{260^\circ}\times 2\times\frac{22}{7}\times 7\\&=\frac{3}{10}\times 2\times 22\\&=13,2\end{align*}$
Jawaban : D
Soal No 9 [UN SMP/MTs 2013]
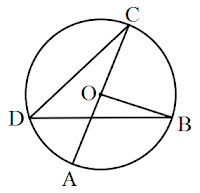
Perhatikan gambar berikut!
Titik $O$ adalah pusat lingkaran. Diketahui $\angle ABE+\angle ACE+\angle ADE=96^\circ$. Besar $\angle AOE$ adalah ....
A. $32^\circ$
B. $48^\circ$
C. $64^\circ$
D. $84^\circ$
Pembahasan:
Perhatikan $\angle ABE$, $\angle ACE$ dengan $\angle ADE$ menghadap busur yg sama, dengan demikian $\angle ABE=\angle ACE=\angle ADE=\frac{96^\circ}{3}=32^\circ$
$\angle AOE$ merupakan sudut pusat yg menghadap busur yg sama dengan sudut keliling $\angle ABE$, $\angle ACE$ dengan $\angle ADE$.
Ingat! sudut pusat $=2\times $ sudut keliling yang menghadap sudut yg sama.
maka:
$\angle AOE=2\times 32^\circ=64^\circ$
Titik $O$ adalah pusat lingkaran. Diketahui $\angle ABE+\angle ACE+\angle ADE=96^\circ$. Besar $\angle AOE$ adalah ....
A. $32^\circ$
B. $48^\circ$
C. $64^\circ$
D. $84^\circ$
Pembahasan:
Perhatikan $\angle ABE$, $\angle ACE$ dengan $\angle ADE$ menghadap busur yg sama, dengan demikian $\angle ABE=\angle ACE=\angle ADE=\frac{96^\circ}{3}=32^\circ$
$\angle AOE$ merupakan sudut pusat yg menghadap busur yg sama dengan sudut keliling $\angle ABE$, $\angle ACE$ dengan $\angle ADE$.
Ingat! sudut pusat $=2\times $ sudut keliling yang menghadap sudut yg sama.
maka:
$\angle AOE=2\times 32^\circ=64^\circ$
Jawaban : C
Soal No 10 [UN SMP/MTs 2012]
Perhatikan gambar!
$P$ adalah titik pusat lingkaran. Luas juring $PLM=24$ $cm^2$, luas juring $PKN$ adalah ....
A. 27 $cm^2$
B. 30 $cm^2$
C. 32 $cm^2$
D. 39 $cm^2$
Pembahasan:
Jadi, luas juring $PKN$ adalah 32 $cm^2$
Jawaban : C
Silakan gabung di Fans Page Facebook, Channel Telegram untuk memperoleh update terbaru, dan Subscribe Channel YouTube m4th-lab untuk memperoleh video pembelajaran matematika secara gratis, untuk mengikuti tautan klik dengan tombol di bawah ini:
m4th-lab Youtube Channel:
m4th-lab Facebook Fans Page:
m4th-lab Telegram Channel:
@banksoalmatematika
Download Ribuan Soal lainnya, lihat pada Daftar Isi atau Klik Disini
Semoga bermanfaat.










Tidak ada komentar:
Posting Komentar