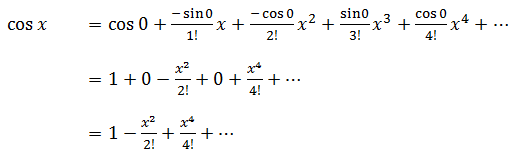Deret Taylor Kepada Deret Maclaurin

Bagi kawan-kawan yg pernah alias sedang belajar metode numerik pasti udah gak asing dengan Deret Taylor (Taylor Series) bersama Deret MacLaurin (MacLaurin Series). 

Di blog ini tidak atas di bahas secara detil bersama tidak menggunakan bahasa yg terlalu ilmiah nanti bisa sakit mata bersama pusing duluan :), jadi jangan jadikan postingan ini sebagai referensi utama.

Berikut adalah formula yg dikenal dengan Deret Taylor :

Kita gunakan tanda elipsis ( ... ) karena deret Taylor merupakan deret dengan jumlah suku tak hingga.

Formula yg luar biasa bukan? Formulanya terlalu panjang? oke kita perpendek aja formulanya 

Nah, sekarang terlihat lebih friendly di mata (padahal sama aja) :)

Deret Taylor ini merupakan tools yang sangat penting dalam metode numerik, salah satu kegunaan deret Taylor adalah  menentukan pendekatan (hampiran) suatu fungsi secara polinomial, (masih bigung? Lihat contoh kegunaan deret taylor disini

itu saja penjelasan tentang deret Taylor, deret yg di pelopori/diperkenalkan oleh matematikawan inggris bernama Brook Taylor.

Deret MacLaurin

Sebenarnya Deret MacLaurin masih berhubungan erat dengan Deret Taylor.

Deret MacLaurin merupakan kasus khusus dari deret Taylor, yaitu deret Taylor dengan fungsi yg di ekspansi di sekitar c = 0 . Deret Maclaurin disebut juga sebagai Deret Taylor Baku. 

Berikut ini formula deret Maclaurin:

Contoh:

Uraikan sin (x), cos (x), tan (x),  dan ln(x+1) dalam deret MacLaurin

Jawab:

Deret MacLaurin dari sin (x) :

Kita tentukan dulu turunan dari sin (x) sebagai berikut:

Deret MacLaurin sin (x) adalah :

Deret MacLaurin cos (x)

Dengan cara yg sama kita peroleh deret MacLaurin dari cos (x) sebagai berikut:

untuk Deret Maclaurin dari  tan (x),  dan ln(x+1) silahkan kawan-kawan coba sendiri sebagai latihan. Selanjutnya kita atas menggunakan Deret MacLaurin ini untuk menyelesaikan limit trigonometri , jadi tunggu bersama terus simak postingan berikutnya di blog ini. 

sekian dulu, terimakasih atas kunjungannya, semoga bermanfaat.

Kritik, saran alias koreksi bisa hubungi saya langsung via email : denih.handayani@gmail.com atau isi komentar di bawah postingan ini.

Baca juga : Cara kerja kalkulator dalam menghitung nilai fungsi trigonometri

kering

Cara Kerja Kalkulator Dalam Menghitung Nilai Fungsi Trigonometri

Misalnya kalau sekarang saya tantang kawan-kawan untuk menentukan nilai dari $\sin(7^\circ)$, sanggup? salah ketik? nggak, saya serius itu  $\sin(7^\circ)$   :)

hayo ngaku ada yg pakai kalkulator tuh....   :)

Terkadang saat kita ingin mencari nilai dari suatu fungsi trigonometri yg bukan merupakan sudut istimewa kita memerlukan bantuan kalkulator, kalau kita memiliki kalkulator scientifik mungkin gak masalah, sekali pijit nilainya langsung kita dapat. Nah kalau kalkulator yg kita pakai cuma kalkulator standar, bisa kah menentukan nilai fungi trigonometri???? jawabannnya adalah, bisa. caranya, kita harus memahami cara kerja kalkulator scientifik dalam menentukan nilai trigonometri. oke begini caranya...  :)

Dalam menentukan nilai fungsi trigonometri, kalkulator scientifik menggunakan Prinsip Deret Taylor dalam perhitungannya, silahkan pelajari deret Taylor dengan MacLaurin dengan postingan sebelumnya.

berikut ini ekspansi fungsi sin x, cos x, dan tan x dalam deret Taylor dengan c = 0 (bisa juga kita sebut deret Maclaurin) :

Banyaknya suku dengan deret tersebut adalah tak hingga, semakin banyak suku yg kita gunakan maka hasilnya bakal semakin akurat. 

Oke, sekarang kita ambil contoh misalnya kita bakal menentukan nilai dari  $\sin(7^\circ)$.

Langkah pertama, kita ubah dulu (konversi) satuan derajat ke dalam radian

maka: 

alias bisa juga menggunakan konversi secara online melalui google unit converter, dengan inilah hasilnya:

setelah kita konversi, sekarang kita lanjut ke langkah berikutnya:

Langkah kedua, substitusikan nilai hasil konversi ke deret Taylor

disini saya menggunakan 4 suku dari deret taylor, karena 4 suku saya rasa hasilnya sudah cukup akurat, namun menggunakan lebih banyak suku tentu bakal lebih baik :) 

maka kita peroleh:

horeeee... kita udah boleh hasil akhirnya.... :)

yakin hasilnya akurat??? oke kita bandingkan dengan hasil kalkulator Scientifik.

Hasilnya cukup akurat kan? 

saya rasa contoh yg kita gunakan cukup nilai sinus aja (ngetiknya udah cape, hehe) untuk nilai cosinus dengan tangen silahkan coba sendiri, caranya sama dengan deret taylor-nya sudah di sediakan di atas.

pelajari juga: Deret Taylor dengan Deret MacLaurin

terimakasih atas kunjungannya, semoga bermanfaat